| La règle
à calcul |
 |
| Historique |
| La règle à
calcul trouve son origine dans le calcul des logarithmes. En effet les
logarithmes inventés par Neper en 1614, sont très
vites devenus indispensables autant pour le calcul numérique,
puisqu'ils permettent de transformer une multiplication en une addition
et que la fonction log est interpolable, que pour l'analyse de phénomènes
physiques ou chimiques; ainsi le noircissement d'une plaque photographique
est donnée par la courbe de Schwarzchild qui dépend
du logarithme du produit de l'intensité lumineuse transmise par
la durée d'exposition (la fonction mathématique correspond
à merveille avec de nombreux phénomènes naturels
et veut dire en quelque sorte "plus le temps passe, plus le phénomène
croit de moins en moins vite".).  Exemple de tables logarithmiques (ici log des nombres de 150 à 159) Pour trouver par exemple log(154.2) , on commence
par inscrire
le nombre 18 (intersection ligne 152 colonne 0), ensuite on prend l'intersection entre la ligne 154 et la colonne 2, soit 808. On obtient alors la partie décimale du nombre cherchée: 18808. Il ne reste plus qu'à prendre comme partie entière le chiffre 2 puisque log(154.2)=log(100*1.542)=log(100)+log(1.542) et que log(100)=2. Donc log(154.2) donne 2.18808. Alors Edmund Gunter, puis William Oughtred
vers 1620 trouvèrent un moyen simple, en traçant des segments
de longueurs proportionnels aux logarithmes des nombres et en faisant
correspondre cette échelle avec l'échelle logarithmique
on trouvait tout de suite le log des nombres. La règle logarithmique
était née. Celle-ci fut fabriquée en de nombreux
matériaux allant du bois à l'ivoire et de différentes
formes. |
| Principe |
Tout le fonctionnement repose sur des échelles
que l'on fait coïncider. Ces échelles peuvent être
simplement millimétriques mais aussi trigonométriques
ou bien encore logarithmiques.  Nous constatons qu'à la valeur 1 de l'échelle B correspond
la valeur 5 de l'échelle A, qu'à la valeur 2 correspond
6 etc. Ainsi nous venons de faire très rapidement l'opération
4+1 puis 4+2...
  Si l'échelle des logs est linéaire (les divisions sont
équidistantes), celle de base est par contre logarithmique. Pourquoi
donc? |
| Multiplication |
| Plus haut on a montré l'exemple des échelles
A et B que l'on fait correspondre pour additionner ou soustraire...
et cette disposition logarithmique de l'échelle de base permet
d'effectuer aussi simplement une multiplication ou division! Voici comment procéder. Tout d'abord les échelles qui
servent sont les deux échelles de base du corps et de la réglette.
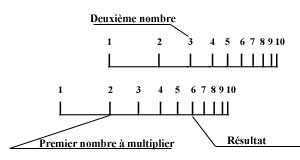 Voici comment trouver le résultat de 2x3
 Le pourquoi de la chose
Si nous cherchons le produit 5x3 le résultat se trouve hors des
limites du corps de la règle. Pour y remédier on utilise
un "déplacement" en affichant le premier nombre avec
le 10 de la réglette, puis on affiche le deuxième nombre
sur la réglette avec le curseur et on lit le résultat sur
le corps de la règle sous le curseur. Ici on lit 1.5 qu'il faut
évidement multiplier par 10 , ce qui donne 15. |
| Division |
La méthode pour diviser n'est guère plus
difficile, il faut d'abord afficher notre dividende sur le corps de la
règle avec le curseur, ensuite on fait glisser la réglette
jusqu'à ce que le diviseur soit sous le curseur. Alors on lit le
résultat en face du 1 de la réglette.  La division 6/3
Même remarque que pour la multiplication, si le dividende est plus petit que le diviseur alors on lit le résultat en face du 10 de la réglette en oubliant pas évidemment, ensuite, de diviser par 10. Avec la pratique le nombre de déplacements pourra être
réduit. Par exemple calculez 4x3x7/6. Le résultat de 4x3x7
que l'on affichera pourra tout de suite être divisé par
6. |
| Autres échelles |
| Généralement les règles
à calcul comprennent 100 subdivisions entre les chiffres 1 et
2 de l'échelle de base (mais cela varie selon la longueur de
la règle). On obtient donc une précision de deux chiffres
après la virgule. Passons maintenant aux échelles trigonométriques. |
| Echelles trigonométriques |
| Tout d'abord selon le type de règle, la méthode
de calcul des sinus et tangentes varie. Ainsi pour les règles
à calcul simples (mais trigonométriques) il est nécessaire
de retourner la réglette en prenant bien soin de faire coïncider
les origines des échelles de base et trigonométriques.
Ensuite il suffit de lire à l'aide du curseur la valeur du sinus
pris sur l'échelle S, sur l'échelle de base - Attention
les échelles trigonométriques sont toujours en degrés
-. Ainsi les règles Rietz permettent de résoudre ce problème en possédant des échancrures au dos de la règle: Une à droite qui servira pour calculer les sinus et sinus-tangentes
et une autre à gauche qui servira à calculer les tangentes.
De plus chaque échancrure dispose d'un fin trait.  On affiche l'angle dans l'échancrure...
 ...et on lit la valeur sur l'autre face de la règle
Par exemple si on a à calculer tan 15 alors on fait correspondre
la valeur 15 avec le trait de l'échancrure gauche. |
| Pour finir |
| Vous aurez remarqué que le curseur comprend
en fait trois traits. Il existe de nombreuses autres subtilités et astuces pour calculer plus rapidement... A vous de les découvrir!  Une partie d'une règle à calcul qui
comprend de gauche à droite: Il n'y a donc pas besoin ici de retourner la règle pour calculer des sinus ou tangentes. |
Copyright 2004 Civitarese Jonathan |
